POVRCHOVÉ A PODZEMNÍ TUNELOVÉ VYTYČOVACÍ SÍTĚ

 

Vytyčovací sítě pro stavbu tunelů se dělí na povrchovou a podzemní část. Jejich budování se řídí požadavky na přesnost tunelových prorážek. Zejména při ražbě podzemního díla z více portálů je požadavek na přesnost vytýčení zcela zásadní. Jakékoliv nedostatky se jen velmi těžko a nákladně napravují. Pro ověření správnosti vytýčení se s výhodou využívají dílčí propojení s povrchem, jinak využívaná pro odvodnění, větrání apod.

 

Účelem povrchové vytyčovací sítě tunelu je získání souřadnicového a výškového propojení mezi charakteristickými body osy tunelu v místě obou portálů s požadovanou přesností. Klasické postupy budování povrchových sítí používají lokální trigonometrickou síť vedenou terénem nad trasou tunelu (Obr. 1). Rekognoskace, stabilizace a zaměření takové sítě bylo náročnou a pracnou záležitostí, zejména v členitém vysokohorském terénu.

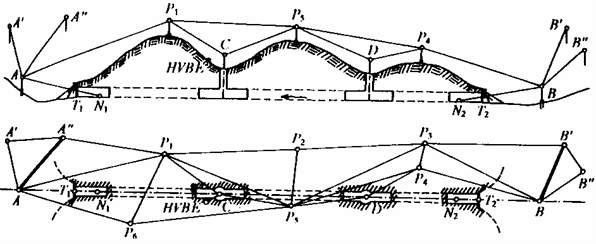
V současné době se k těmto účelům využívá technologie globálních polohových systémů (GNSS). Tato technologie nepotřebuje vzájemnou viditelnost mezi jednotlivými body, které se zřizují pouze v místech vstupních objektů (portálů, šachet, štol – viz Obr. 1).

 

Podzemní tunelová vytyčovací síť je tvořena volným polygonovým pořadem jednostranně připojeným a orientovaným pomocí bodů portálové sítě, postupně prodlužovaným až k místu tunelové prorážky. Koncové body tohoto pořadu jsou používány k vytyčování směru při ražení. Podzemní vytyčovací pořady jsou většinou přímé a rovnostranné.

 

ROZBOR PŘESNOSTI TUNELOVÉ PRORÁŽKY

 

Požadavky na přesnost tunelové prorážky jsou určeny druhem a projektovými parametry tunelu, technologií jeho výstavby a požadavky liniové stavby pro kterou se tunel buduje. Skutečná přesnost prorážky je ovlivněna přesností povrchové vytyčovací sítě, přesností připojovacího měření v místech vstupních objektů a přesností podzemní vytyčovací sítě. Mezní odchylky prorážky jsou stanoveny v [9].

 

Tunelová osa se zpravidla vytyčuje ze dvou protilehlých směrů (čelba a protičelba). Celková mezní odchylka prorážky d_M je odvozena ze stavební tolerance T podle vztahu T = 5d_M, používá se též poměru T = 2 d_M. Protože odchylka ve směru osy tunelu je méně významná, bývá obvyklé rozdělit celkovou odchylku d_M mezi příčnou ( d_q ) a výškovou ( d_h) složku:

Výšková měření lze zpravidla vykonat s vyšší přesností, volí se mezi oběma složkami poměr např.

d_q = 2d_h, což po dosazení do předchozího vztahu dává

Za předpokladu vytyčování místa prorážky dvěma protisměrnými polygonovými pořady o stejném počtu vrcholů tedy bude pro požadovanou střední chybu jedné větve platit vztah

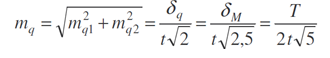
kde m_q1 je střední chyba vyjadřující vliv přesnosti povrchové sítě a m_q2 je střední chyba vyjadřující vliv přesnosti podzemního prorážkového pořadu včetně jeho připojení na povrchovou síť. V praxi je nutné zvolit optimální poměr obou těchto složek.

VYTYČOVÁNÍ PŘI RAŽBĚ TUNELŮ

 

Základem pro rozbory přesnosti vytyčení osy tunelu v podzemí je teorie rozborů přesnosti polygonových pořadů. Prorážkový bod je vytyčován jako koncový bod podzemního volného polygonového pořadu, který je připojen a orientován na body portálové sítě. Úloha může být interpretována jako „postupný rajon“.

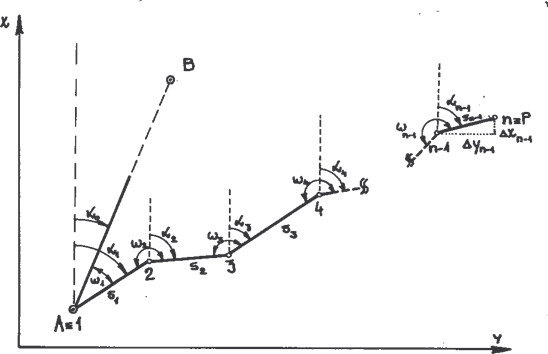
Při vytyčení prorážkového bodu volným polygonovým pořadem se pracuje s následujícími daty:

Výchozí data: souřadnice výchozího bodu A [ x_A , y_A ],

orientační směrník α₀

Měřené veličiny: vrcholové úhly Ѡ_i        ( i = 1, 2, , n-1) ,

délky stran  s_i               ( i = 1, 2, , n-1).

Určované parametry: souřadnice vytyčovaného bodu P [ x , y ]

Poloha vytyčeného bodu je určena dvojicí souřadnic x , y podle vztahů

(označení veličin viz Obr. 2)

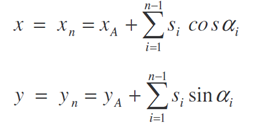
Směrníky jednotlivých stran α_i jsou funkcemi orientačního směrníku a měřených

vrcholových úhlů Ѡ_i . Jejich určující vztahy jsou (dle Obr. 49)

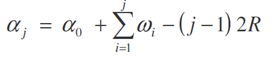
Skutečné chyby v souřadnicích koncového bodu pořadu lze vyjádřit vztahy

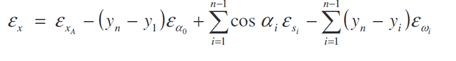
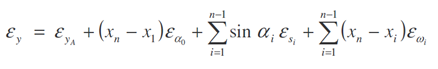
Uplatněním zákona přenosu středních chyb a kovariancí lze napsat vztahy pro prvky kovarianční matice vytyčeného bodu:

střední chyby jednotlivých souřadnic

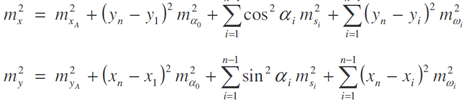
kovariance

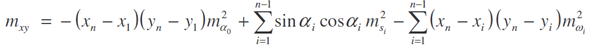
střední souřadnicová chyba

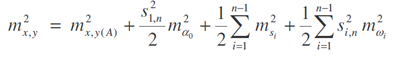
V praktických případech jsou často splněny podmínky stejné úrovně přesnosti měření délek stran pořadu (m_s1 ≈ m _≈ ……….m_{sn-1  =} m_s ) a stejné úrovně přesnosti měření vrcholových úhlů (m_Ѡ1 ≈ m_Ѡ2  ≈ ………. m_Ѡn-1 = m_Ѡ ) a předcházející vzorce pak přejdou na jednodušší tvar:

střední chyby jednotlivých souřadnic

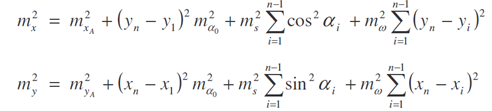
kovariance

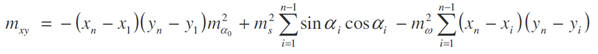
střední souřadnicová chyba

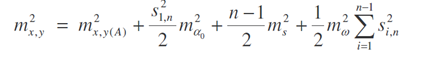
Zvláštním případem tohoto typu polygonového pořadu je přímý pořad, kde hodnoty vrcholových úhlů Ѡ_i = 2R pro i ≥ 2 . Jestliže navíc platí další podmínka s₁ = s₂ = …… = s_n-1 = s , jedná se o pořad rovnostranný (viz Obr. 3).

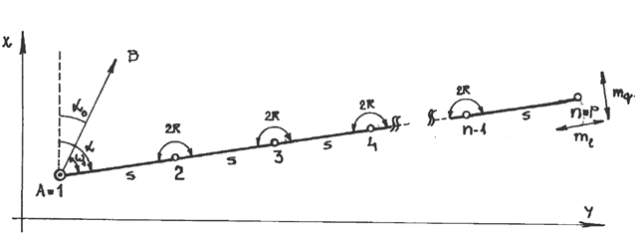
Pro takový tvar volného polygonového pořadu lze odvodit jednodušší vztahy pro přesnost koncového bodu pořadu v podélném a příčném směru:

skutečná chyba podélná (ve směru pořadu)

střední chyba příčná (kolmo ke směru pořadu)

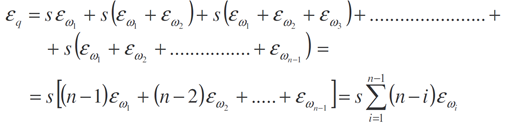
Za předpokladu stejné úrovně přesnosti měření délek stran s a vrcholových úhlů Ѡ_i jsou pak střední chyby dány výrazy

střední chyba podélná

střední chyba příčná

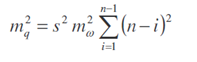
kterou lze sečtením číselné řady upravit na konečný tvar

Pro pořady s počtem vrcholů n > 6 lze použít bez podstatné újmy na přesnosti ještě jednodušší vzorec pro střední chybu příčnou ve tvaru

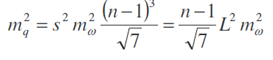
kde L = s (n – 1) je celková délka pořadu.

V praktických případech někdy nebývá splněn předpoklad stejných délek stran pořadu. Pak je obvyklé dosazovat za  s  průměrnou délku strany

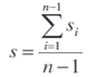
Poznámka: Analýza odvozených vzorců pro rozbory přesnosti polohy bodu vytyčeného volným polygonovým pořadem ukazuje, že chyby rostou se zvětšující se délkou pořadu. Pokud je alespoň přibližně splněn předpoklad přímosti pořadu, pak je pro velikost podélné chyby na konci pořadu rozhodující přesnost délkového měření a pro velikost příčné chyby je rozhodující přesnost úhlového

měření. Pro předběžné orientační rozbory přesnosti se dají velmi dobře použít vzorce pro přímý rovnostranný pořad. Jsou-li kladeny zvýšené požadavky na přesnost vytyčení v příčném směru, doporučuje se použití trojpodstavcové soupravy pro omezení vlivu centračních chyb (důlní prorážkové pořady apod.). Při vysokých nárocích na spolehlivost se některé strany pořadu orientují pomocí gyroteodolitu.

Při vytyčování přímých tunelů se používá vzorec pro výpočet příčné střední chyby koncového bodu přímého rovnostranného pořadu v příčném směru

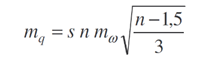
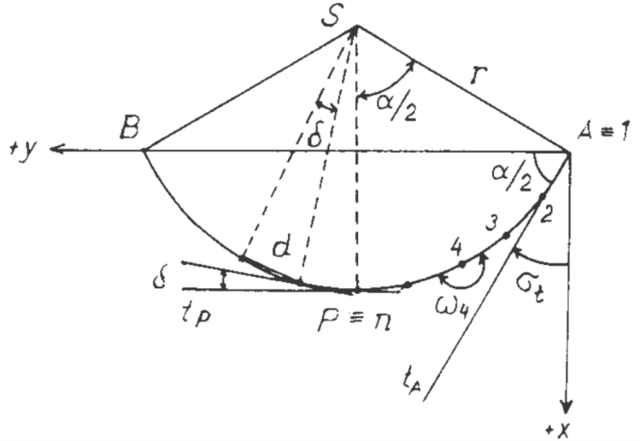
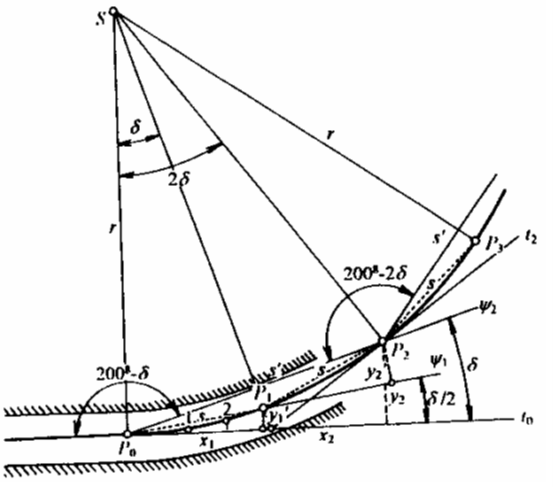
Při vytyčování tunelů v oblouku se používají upravené vzorce pro rozbor přesnosti obecného polygonového pořadu. Při označení veličin podle Obr. 11 a za předpokladu rovnostranného pořadu platí pro střední chybu koncového bodu ve směru normály (příčném) vztah [Obr. 4]

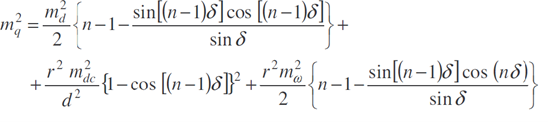
kde d je délka strany obloukového polygonového pořadu, d je středový úhel odpovídající této délce, r je poloměr oblouku, Ѡ je vrcholový úhel, n je počet vrcholů pořadu, m²_Ѡ je střední chyba vrcholového úhlu, m²_d je náhodná složka střední chyby délky a m²_dc je její systematická složka. Pro střední chybu ve směru tečny (podélném) platí vztah

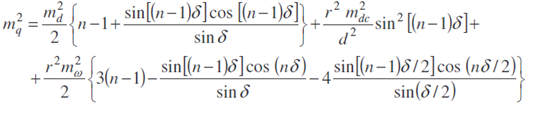
VYTYČENÍ OBLOUKU TRASY KOMUNIKACE V TUNELU

 

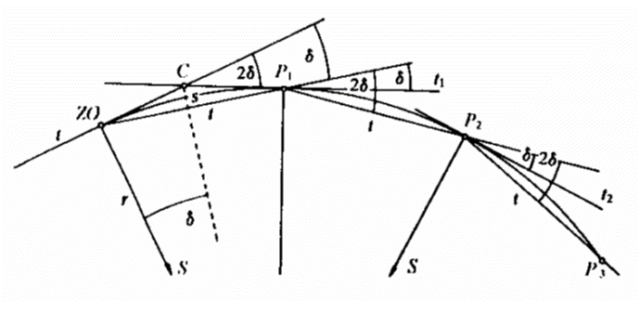
Při vytyčování oblouků trasy v tunelu se používá metoda přenášení přístroje po obvodě oblouku (viz Obr. 5) nebo metoda postupného odbočování od tětivy (viz Obr. 6):

 

Zdroj:

Geodézie v podzemních prostorách, HE 08 Modul 02, Měření podzemních inženýrských staveb, prof. Ing. Otakar Švábenský, CSc., doc. Ing. Jiří Bureš, Ph.D., doc. Ing. Vladislav Horák, CSc., Ing. Alexej Vitula